Answer:
Final velocity, V = 2.1213 m/s.
Step-by-step explanation:
Given the following data;
Force, F = 1.50N
Mass, m = 0.2kg
Displacement, S = 30cm to meters = 30/100 = 0.3m
To find the acceleration;
Force is given by the multiplication of mass and acceleration.
Mathematically, Force is given by the formula;
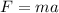 .......equation 1
.......equation 1
Where;
- m represents the mass of an object.
- a represents acceleration.
Making acceleration (a) the subject, we have;
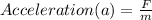
Substituting into the above equation, we have;
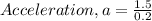
Acceleration, a = 7.5m/s²
Now to find the final velocity, we would use the third equation of motion;
 .....equation 2
.....equation 2
Where;
- V represents the final velocity measured in meter per seconds.
- U represents the initial velocity measured in meter per seconds.
- a represents acceleration measured in meters per seconds square.
- S represents the displacement measured in meters.
Note: Since the trolley is starting from rest, we know that it's initial velocity is 0.
Substituting the values into equation 2, we have;
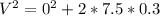
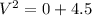
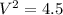
Taking the square root, we have;
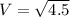
V = 2.1213 m/s.
Therefore, the speed of the trolley after accelerating from rest through 0.3 m, if friction is negligible is 2.1213 m/s.