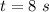Question

You are piloting a helicopter which is rising vertically at a uniform velocity of 14.70 m/s. When you reach 196.00 m, you see Barney (Uh-oh). A large object is projected with a horizontal velocity of 8.50 m/s from the rising helicopter. When does the ball reach Barney's head if he is standing in a hole with his head at ground level?

Answer 1

The ball reaches Barney head in
`t = 8 \ s`

Step-by-step explanation:

From the question we are told that

The rise velocity is
`v = 14.70 \ m/s`

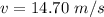
The height considered is
`h = 196 \ m`

The horizontal velocity of the large object is
`v_h = 8.50 \ m/s`

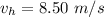
Generally from kinematic equation

`s = ut + (1)/(2) gt^2`

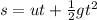
Here s is the distance of the object from Barney head ,

u is the velocity of the object along the vertical axis which is equal but opposite to the velocity of the helicopter

So

`u = -14.7 m/s`

So

`196 = -14.7 t + (1)/(2) * 9.8 * t^2`

=
`4.9 t^2 - 14.7t - 196 = 0`

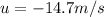
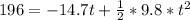
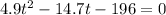
Solving the above equation using quadratic formula

The value of t obtained is
`t = 8 \ s`