Answer:
Cherries cost $2.50 per pound
Yes, it is constant.
Weight would go on the x-axis and the cost would go on the y-axis.
The two points are (2, 5) and (3, 7.5)
5 pounds of cherries would cost $12.50. To solve the problem I multiplied the 5 pounds by 2.5, the cost per pound to find the cost.
Explanation:
$5 for 2 pounds and $7.50 for 3 pounds can be turned into the points (2, 5) and (3, 7.5).
To find the cost per pound, input the two points into the slope formula:
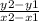

Solve:
7.5 - 5 = 2.5
3 - 2 = 1
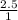 = 2.5
= 2.5
The cost of cherries per pound is $2.50. This is our slope.
The equation that represents the cost of cherries for x amount of pounds is:
y = 2.5x
To find how much 5 pounds of cherries would cost, replace x with 5 in the equation:
y = 2.5(5)
y = 12.5
5 pounds of cherries would cost $12.50.
I hope this helps :)