Question

Find the value of n for which the vectors a⃗ =(3,2)a→=(3,2) and b⃗ =(9,n)b→=(9,n) are collinear.​

Answer 1

For n=6, the given vectors will be collinear.

Explanation:

Collinear vectors are the vectors which lie on the same line or parallel lines. In order to find if two vectors are collinear, their ratio is found. If the ratio is same for all unit vectors then the vectors are collinear.

Given

`a = (a_1, a_2) = (3,2)\\b = (b_1, b_2) = (9,n)`

The ratio of first unit vectors is:

`(a_1)/(b_1) = (3)/(9) = (1)/(3)`

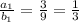
In order for the vectors to be collinear the other ratio should also be 1/3

`(a_2)/(b_2) = (1)/(3)`

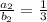
Writing it mathematically

`(2)/(n) = (1)/(3)\\2*3 = n\\n = 6`

Hence,

For n=6, the given vectors will be collinear.