Question

If a toy rocket is launched vertically upward from the ground level with an initial velocity of 128 feet per second, then its height h after t seconds is given by the equation:

h(t) = -16t^2 + 128t
What is the maximum height the rocket reaches?

Answer 1

The maximum height of the rocket is 256 feet

Explanation:

The vertex form of the quadratic function f(x) = ax² + bx + c is

f(x) = a(x - h)² + k, where

• (h, k) is the vertex point

• h =
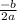  `(-b)/(2a)` and k = f(h)

• (h, k) is a minimum point if a > 0 and a maximum point if a < 0

Let us use these rules to solve the question

∵ h(t) = -16t² + 128t

→ Compare it by the form of the quadratic function above

∴ a = -16 and b = 128

∵ a < 0

∴ The vertex (h, k) is a maximum point

∴ The maximum height of the rocket is the value of k

→ Use the rule of h above to find it

∵ h =
`(-128)/(2(-16))` =
`(-128)/(-32)`

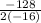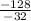
∴ h = 4

→ Substitute x in the equation by the value of h to find k

∵ k = h(h)

∴ k = -16(4)² + 128(4)

∴ k = -256 + 512

∴ K = 256

∴ The maximum height of the rocket is 256 feet