Question

Apples: $(2x) per pound

Grapes: $(6x – 5) per pound
Oranges: $(x + 2) per pound
A shopper purchases one pound each of
apples, grapes, and oranges and spends
$10.50. How much is spent on each type
of fruit?

Answer 1

Shopper spend $3 on Apples, $4 on Grapes and $3.5 on Oranges

Explanation:

Cost of one pound of Apple = $2x

Cost of one pound of Grapes = $(6x-5)

Cost of one pound of Oranges = $(x+2)

A shopper purchases one pound each of apples, grapes, and oranges and spends $10.50.

It can be written as:
`2x+6x-5+x+2=10.50`

We need to find how much the shopper spend on each fruit.

First we need to find value of x by solving equation

`2x+6x-5+x+2=10.50`

Solving:

`2x+6x+x+2-5=10.50\\9x-3=10.50\\9x=10.50+3\\9x=13.5\\x=(13.5)/(9)\\x=1.5`

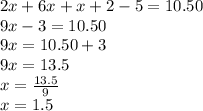
The value of x is: x=1.5

Now finding cost of one pound each fruit by putting x=1.5

Cost of one pound of Apple = $2x = 2(1.5) = $3

Cost of one pound of Grapes = $(6x-5) = (6(1.5)-5)= $4

Cost of one pound of Oranges = $(x+2)=(1.5+2)=$3.5

So,

Cost of one pound of Apple = $3

Cost of one pound of Grapes = $4

Cost of one pound of Oranges = $3.5

So, shopper spend $3 on apples, $4 on Grapes and $3.5 on Oranges