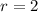Question

The first three teams in a geometric sequence are a – 2, a, a + 4, What is the common ratio of

be sequence?​

Answer 1

2

Explanation:

solution at attachment box

a2/a1 =r

a3/a2=r

Answer 2

Please check the explanation.

Explanation:

Given the geometric sequence

a – 2, a, a + 4

• We know that the common ratio 'r' of a geometric sequence can be obtained by dividing the successor term by the previous term.

• Also, we know that the common ratio 'r' of a geometric sequence is the same i.e. remain constant.

so the expression to find the common ratio 'r' of the geometric sequence will be:

`\:r` ⇒
`(a)/(a-2)=(a+4)/(a)`

`(a)/(a-2)=(a+4)/(a)`

`\mathrm{Apply\:fraction\:cross\:multiply:\:if\:}(a)/(b)=(c)/(d)\mathrm{\:then\:}a\cdot \:d=b\cdot \:c`

`aa=\left(a-2\right)\left(a+4\right)`

`a^2=\left(a-2\right)\left(a+4\right)`

`a^2=a^2+2a-8`

`\mathrm{Subtract\:}a^2+2a\mathrm{\:from\:both\:sides}`

`a^2-\left(a^2+2a\right)=a^2+2a-8-\left(a^2+2a\right)`

`-2a=-8`

`\mathrm{Divide\:both\:sides\:by\:}-2`

`(-2a)/(-2)=(-8)/(-2)`

`a=4`

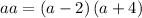
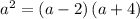
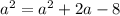
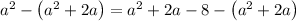
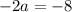
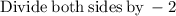
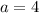
so the ratio becomes

`r=\:(4)/(4-2)=(4)/(2) =2`

Hence, the common ratio 'r' will be:

`r=2`

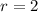
VERIFICATION

so the sequence becomes

a – 2, a, a + 4

(4) - 2, 4, (4)+4 ∵ a=4

2, 4, 8

From the sequence it is clear that

4/2=8/4 ⇒ r

2=2 ⇒ r

Hence, the common ration 'r=2' is the same.

Therefore, the common ratio 'r' will be:

`r=2`