Question

FIND THE AREA OF THE SEGMENT AYB. IF RADIUS OF THE CIRCLE IS 21cm AND ANGLE AOB= 120 DEGREE ( use pie= 22/7)

PLZ answer very urgent

Answer 1

The area of the segment AYB is 271.0413985 cm²

Explanation:

The rule of the area of a sector is A =
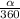`(\alpha )/(360)` × π r², where

• α is the central angle of the sector

• r is the radius of the circle

The area of a triangle is A =
`(1)/(2)` × s1 × s2 × sinФ

• s1 and s2 are two sides of the triangle

• Ф is the included angle between s1 and s2

∵ Area of the segment AYB = Area the sector AOB - Area ΔAOB

∵ The radius of the circle is 21 cm

∴ r = 21 cm

∵ The central angle of the sector is 120°

∴ α = 120°

∵ π =
`(22)/(7)`

→ Substitute them in the rule of the area of the sector to find it

∵ Area sector AOB =
`(120)/(360)` ×
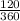`(22)/(7)` × (21)²

∴ Area of sector AOB = 462 cm²

∵ OA and OB are the radii of the circle

∴ s1 = OA and s2 = OB

∴ s1 = s2 = 21 cm

∵ The angle included between them is 120°

∴ Ф = 120°

→ Substitute them in the rule of the area of the triangle to find it

∵ Area of the Δ =
`(1)/(2)` × 21 × 21 × sin(120)

∴ Area of the Δ = 110.25√3 cm²

∵ Area of the segment AYB = Area the sector AOB - Area ΔAOB

∴ Area of the segment AYB = 462 - 110.25√3

∴ Area of the segment AYB = 271.0413985 cm²