Answer:
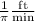 is the rate at which the water is rising when the water is 6 ft deep.
is the rate at which the water is rising when the water is 6 ft deep.
Explanation:
See the attached diagram that I drew to represent this problem.
To solve related rates problems, let's use the recommended steps:
- Draw a diagram.
- Label all quantities and their rates of change.
- Relate all quantities in the same equation.
- Differentiate (implicitly) with respect to time.
- Use the resulting equation to answer the question in context.
Step 1:
I already drew the diagram; see attached image.
Step 2:
I labeled the quantities we are given in the problem. h = 10 ft, and r = 5 ft. We are also told that the change in volume is 9 ft³/min; dV/dt = 9 ft³/min.
We want to find dh/dt when h = 6.
Step 3:
We know that we are dealing with a cone in this problem, and we are given the volume of the cone. Therefore, we can use the formula for the volume of a cone in order to relate all of the quantities in the same equation.
Since we only want the two variables, V and h, we can solve for r in terms of h and substitute this value for r in the formula.
This is because when we perform implicit differentiation, we do not have the change in r (dr/dt) but we do have dh/dt, which is what we are trying to solve for.
We know that r = 5 ft, and h = 10 ft. Therefore, we can say that
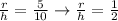 . Multiply h to both sides to solve for the variable r:
. Multiply h to both sides to solve for the variable r:
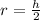 .
.
Substitute this into the volume of a cone equation:
Simplify this equation.
Step 4:
Perform implicit differentiation on the volume equation.
Step 5:
Substitute known values and solve for dh/dt to find the change in height, or the rise in water level, when the water is 6 ft deep (h = 6).
We know that:
Plug these values into the implicitly differentiated volume equation.
Answering the question in context:
Since dh/dt = 1/π when h = 6 ft, we can say that the water is rising at a rate of
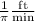 when the water is 6 ft high.
when the water is 6 ft high.