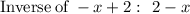Question

What is the inverse of fx) =

-x+ 2?
O h(x) =
) = 4x+2
O h(x) = = -x-2
3
O h(x) = 3x - 2
h(x) = 3x - 6

Answer 1

Note: Your statement and answer options are a little ambiguous, so I am assuming you want to determine the inverse of f(x)=-x+2.

As the process is the same, so it would still clear your concept.

Answer:

`\mathrm{Inverse\:of}\:-x+2:\:\:2-x`

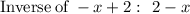
Explanation:

Given the function

`f(x)=-x+2`

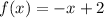
• We know that a function h is the inverse function of f if for y=f(x), x=h(y)

Determining the inverse

`y=-x+2`

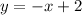
Replace x with y

`x=-y+2`

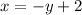
solve for y

`y=2-x`

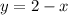
Therefore,

`\mathrm{Inverse\:of}\:-x+2:\:\:2-x`