2 Answers

Jnemecz · Answer 1 · 2021-08-22T15:38:56+0000

Answer:

The equation of the line that passes through the points (-1,8) and (2,-4) is:

Explanation:

Given the points

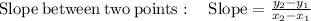
$\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

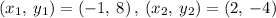
$\left(x_1,\:y_1\right)=\left(-1,\:8\right),\:\left(x_2,\:y_2\right)=\left(2,\:-4\right)$

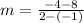
$m=(-4-8)/(2-\left(-1\right))$

m=-4

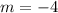
As the point-slope form of the line equation is

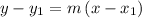
$y-y_1=m\left(x-x_1\right)$

where m is the slope.

substituting the values m = -4 and the point (-1,8)

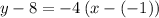
$y-\(8\right=-4\left(x-\left(-1\right)\right)$

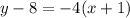
y-8 = -4(x+1)

Add 8 to both sides

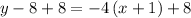
$y-8+8=-4\left(x+1\right)+8$

y=-4x+4

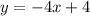
Therefore, the equation of the line that passes through the points (-1,8) and (2,-4) is:

Please log in or register to add a comment.