Answer:
a. ST and UV are perpendicular lines.
b. BC and DE are parallel.
c. NP and QR are neither parallel nor perpendicular.
d. GH and JK are parallel.
Explanation:
Slopes are used to calculate steepness of a line. Slopes are also used to check if two lines are parallel, perpendicular or neither.
When two lines are parallel, their slopes are equal.
When two lines are perpendicular, product of slopes of both lines is -1
Slope is given by the formula:
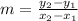
a) S(-4, -1), T(-1,5) and U(1,1), V(5, -1)
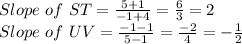
Now,
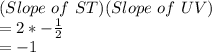
ST and UV are perpendicular lines.
b) B(-6, -2), C(-3, 3) and D(2,0), E(5,5)

As the slopes of two lines is equal, BC and DE are parallel.
c) N(-6,2), P(--3, -4) and Q(1, -3), R(3, 4)

NP and QR are neither parallel nor perpendicular.
d) G(-2,5), H(4,1) and J(1, –4), K(7,0)
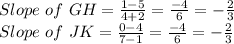
GH and JK are parallel.
Hence,
a. ST and UV are perpendicular lines.
b. BC and DE are parallel.
c. NP and QR are neither parallel nor perpendicular.
d. GH and JK are parallel.