Question

Reflection across y= -x

Answer 1

option A) is correct.

Explanation:

As we know that when we reflect across the line
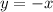`y=-x`, the x-coordinate and y-coordinate would change places and be negated.

So the formula about the reflection across
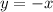`y=-x` will be:

(x, y) ⇒ (-y, -x)

From the graph, the vertices of the triangle are:

• Vertex U = (-5, -2)

• Vertex T = (-3, -3)

• Vertex V = (-5, -5)

As the rule of reflection across
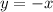`y=-x` will produce the image with the vertices T', U' and V' which are as follows:

(x, y) ⇒ (-y, -x)

• U(-5, -2) ⇒ (-y, -x) = U' (2, 5)

• T(-3, -3) ⇒ (-y, -x) = T' (3, 3)

• V(-5, -5) ⇒ (-y, -x) = V' (5, 5)

So, the vertices of U', T' and V' will be:

• U' (2, 5)

• T' (3, 3)

• V' (5, 5)

Therefore, option A) is correct.