Answer:
Solving this system of linear equations by elimination we get x=-1 and y=-2
Option 1 is correct option.
Explanation:
We are given equations:

We need to solve by Elimination method.
Elimination method: Add or subtract the equations to get an equation in one variable.
Rearranging the equation 1 we get
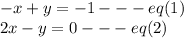
Add eq(1) and eq(2)
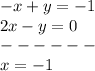
So, after eliminating y we get x=-1
Now finding y by putting x in eq(1)

We get y=-2
So, solving this system of linear equations by elimination we get x=-1 and y=-2
Option 1 is correct option.