Question

10/3 * 3^x -3^(x-1) = 81
Solve for x.​

Answer 1

`\boxed{ \rm \: x = 3}`

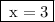
Explanation:

Equation given:

10/3 × 3^x -3^(x-1) = 81

Finding the value of x :

`\implies \rm \: \cfrac{10}{3} * 3 {}^(x) - \cfrac{3 {}^(x) }{3} = 81`

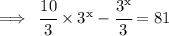
• (We took 3^x-1 as 3^x/3 because according law x^m-n = x^m/x^n)

`\implies \rm \cfrac{10 * 3 {}^(x) }{3} - \cfrac{3 {}^(x) }{3} = 81`

`\implies \rm \cfrac{10 * 3 {}^(x) - 3 {}^(x) }{3} = 81`

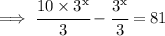
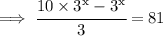
Taking 3x common,we get:

`\implies \rm \cfrac{3 {}^(x)(10 - 1) }{3} = 81`

`\implies \rm3 {}^(x) * \cfrac{ \cancel9}{ \cancel{3} } = 81`

`\implies \rm3 {}^(x) * 3 = 81`

`\implies \rm {3}^(x) = \cfrac{ \cancel{81} \: {}^(27) }{ \cancel3}`

`\implies \rm3 {}^(x) = 3 {}^(3)`

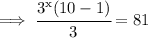
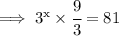
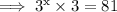
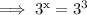
Since according to the law of exponents,if the bases are equal then the powers are equal too.

`\implies \rm{x} = \boxed3`

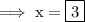
Hence,the value of x is 3.

Answer 2

`x=3`

Explanation:

`~~~~~~~(10)/(3) \cdot 3^x - 3^(x-1) = 81\\\\\\\implies 10 \cdot 3^(x-1) - 3^(x-1) = 81~~~~~~~~~~~~~~~~~~~~;\left[(a^m)/(a^n) =a^(m-n) \right]\\\\\\\implies 9\cdot 3^(x-1) = 81\\\\\\\implies 3^(x-1) = (81)/(9)\\\\\\\implies 3^(x-1) = 9\\\\\\\implies 3^(x-1) = 3^2\\\\\\\implies x -1 = 2\\\\\\\implies x = 2+1\\\\\\\implies x = 3`