Question

The scores for all high school seniors taking the verbal section of the Scholastic Aptitude Test (SAT) in a particular year had a mean of 490 and a standard deviation of 100. The distribution of SAT scores is bell-shaped.

What percentage of seniors scored between 390 and 590 on this SAT test?

Answer 1

The value is
`P( 390 < X < 590) = 68.3 \%`

Explanation:

From the question we are told that

The mean is
`\mu = 490`

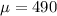
The standard deviation is
`\sigma = 100`

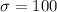
Generally the proportion of seniors scored between 390 and 590 on this SAT test is mathematically represented as

`P( 390 < X < 590) = P( (390 - 490 )/(100) < (\= x - \mu )/(\sigma) < (590 - 490 )/( 100) )`

`(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )`

`P( 390 < X < 590) = P( -1 < Z < 1 )`

=>
`P( 390 < X < 590) = P(Z< 1 ) - P(Z < - 1 )`

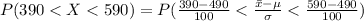
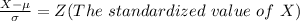
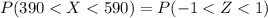
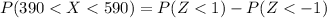
From the z table the area under the normal curve to the left corresponding to 1 and -1 is

`P(Z< 1 ) = 0.84134`

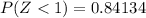
and

`P(Z< - 1 ) = 0.15866`

`P( 390 < X < 590) =0.84134 - 0.15866`

=>
`P( 390 < X < 590) = 0.6827`

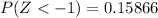
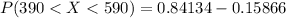
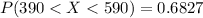
Generally the percentage of seniors scored between 390 and 590 on this SAT test is mathematically represented as

=>
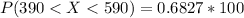
`P( 390 < X < 590) = 0.6827 *100`

=>
`P( 390 < X < 590) = 68.3 \%`