Question

A park is showing a movie on the lawn. The base of the screen is 6 feet off the ground and the screen is 22 feet high (see figure).

Answer 1

A. 61.82°;

15.64°

B. 33.37°

Explanation:

A.

✍️Angle of elevation from 15 ft:

A right triangle is formed. Apply trigonometric ratios formula to find the angle of elevation from 15 ft.

Thus,

Length of the side Opposite to reference angle = 22 + 6 = 28 ft

Adjacent length = 15 ft

Thus, we would have:

`tan(\theta) = (opp)/(adjacent) = (28)/(15)`

`tan(\theta) = 1.8667`

`\theta = tan^(-1)(1.8667)`

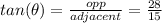
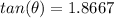
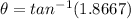
`\theta = 61.82` (2 d.p)

✍️Angle of elevation from 100 ft:

Thus,

Length of the side Opposite to reference angle = 22 + 6 = 28 ft

Adjacent length = 100 ft

Thus, we would have:

`tan(\theta) = (opp)/(adjacent) = (28)/(100)`

`tan(\theta) = 0.28`

`\theta = tan^(-1)(0.28)`

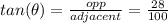
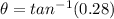
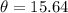`\theta = 15.64` (2 d.p)

B.

✍️Distance you'd be from the screen if you lie on the ground and make an angle of elevation of 40° to the top of the screen:

Adjacent length = your distance from the screen = x

Opposite length = 22 + 6 = 28 ft

Angle of elevation = 40°

Tge trigonometric ratios formula to use would be:

`tan(\theta) = (opp)/(adjacent)`

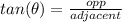
Plug in the values

`tan(40) = (28)/(x)`

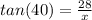
Multiply both sides by x

`x*tan(40) = 28`

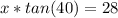
Divide both sides by tan(40)

`x = (28)/(tan(40))`

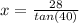
`x = 33.37` (2 d.p)