Question

20 points! o(*￣▽￣*)\

Write a linear equation in slope-intercept form to represent the data shown in this table.
Bicycle Rental Costs
Time, x(hours) Total cost, y(dollars)
1 $8
2 $16
3 $24

Show your work.

Answer 1

Answer:I believe its y=8x or y=8

Answer 2

`\displaystyle y=8x`

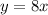
Explanation:

We are given a table and we want to determine a linear equation (in slope-intercept form) that represents this table.

So, we will first need to determine the slope. We can use the slope formula:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

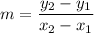
Where (x₁, y₁) and (x₂, y₂) are two points.

We have three points: (1, 8), (2, 16), and (3, 24).

Let’s pick two. We can use (1, 8) and (2, 16).

So, let (1, 8) be (x₁, y₁) and let (2, 16) be (x₂, y₂). Substitute appropriately:

`\displaystyle m=(16-8)/(2-1)`

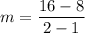
Evaluate:

`\displaystyle m=(8)/(1)=8`

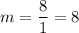
So, our slope is 8.

Now, we can determine the equation using point-slope form:

`\displaystyle y-y_1=m(x-x_1)`

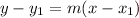
Where m is our slope and (x₁, y₁) is a point.

We know that the slope is 8, so we will substitute 8 for m.

We can use any of our three points for the point. Let’s use (1, 8) for consistency. So, let (1, 8) be (x₁, y₁). Substitute appropriately:

`\displaystyle y-8=8(x-1)`

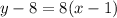
Solve for y. Distribute the right:

`\displaystyle y-8=8x-8`

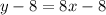
Add 8 to both sides:

`\displaystyle y=8x`

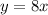
And we have our equation.

Notice that this is a direct variation or proportional equation as we don’t have a y-intercept.