Final Answer:
The diagonals AC and BD of rectangle ABCD are congruent. The length of AC is equal to BD. The length of BD is equal to AC.
Step-by-step explanation:
In a rectangle, opposite sides are parallel, and adjacent sides are perpendicular. Let's consider the coordinates of the vertices A(0, 0), B(a, 0), C (x, y), and D (0, b). Since ABCD is a rectangle, we know that AB is parallel to CD and BC is parallel to AD, and AB is perpendicular to BC and AD.
The length of AC can be calculated using the distance formula:
AC =
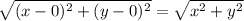
Similarly, the length of BD can be calculated as:
BD =
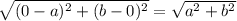
Now, since AC and BD are both diagonals of the rectangle, if we can show that
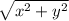 =
=
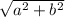 , then the diagonals are congruent.
, then the diagonals are congruent.
Consider the rectangle's properties: AB and CD are parallel, so a = x, and AD and BC are parallel, so b = y. Therefore,
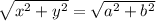 simplifies to
simplifies to
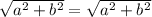 , confirming that the diagonals AC and BD are indeed congruent.
, confirming that the diagonals AC and BD are indeed congruent.