Question

The value of y varies directly with x, and y = 5 when x = -20. Find y when x = 35.

Please help! Thanks!!!!

Answer 1

Explanation:

If y= -5 when x= -20 that means x is 4 times y

y= 8.75 when x= 35

Answer 2

Our equation is:

`\displaystyle y=-(1)/(4)x`

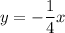
When x=35, y=-35/4 or -8.75.

Explanation:

We know that y varies directly with x.

The standard equation is:

`y=kx`

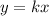
We know that y is 5 when x is -20.

So, let’s substitute 5 for y and -20 for x and solve for k, our constant of variation. So:

`5=k(-20)`

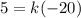
Divide both sides by -20:

`\displaystyle k=-(1)/(4)`

Therefore, our constant of variation is -1/4.

Hence, our equation is:

`\displaystyle y=-(1)/(4)x`

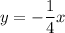
To find y when x=35, let’s substitute 35 for x. So:

`\displaystyle y=-(1)/(4)(35)=-(35)/(4)=-8.75`

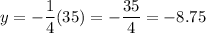
So, when x=35, y=-8.75.