Question

A lifeguard is in an observation chair and spots a person who needs help. The angle of depression to the person is 22°. The eye level of the lifeguard is 10 feet above the ground. What is the horizontal distance between the lifeguard and the person? Round to the nearest foot.

Answer 1

The horizontal distance between the lifeguard and the person is approximately 24.751 feet.

Explanation:

At first we include a geometrical representation of the statement, which is shown in the image attached below. We can determine the horizontal distance between the lifeguard and the person by means of the following trigonometrical relationship:

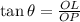`\tan \theta = (OL)/(OP)` (1)

Where:

`\theta` - Angle of depression to the person, measured in sexagesimal degrees.

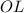`OL` - Height of the lifeguard above the ground, measured in feet.

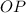`OP` - Horizontal distance between the lifeguard and the person, measured in feet.

If we know that
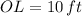`OL = 10\,ft` and
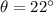`\theta = 22^(\circ)`, then the horizontal distance between the lifeguard and the person is:

`OP = (OL)/(\tan \theta)`

`OP = (10\,ft)/(\tan 22^(\circ))`

`OP \approx 24.751\,ft`

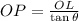
The horizontal distance between the lifeguard and the person is approximately 24.751 feet.