Question

Approximate the root by using a linearization centered at an approximate nearby number
√101

Answer 1

Context:

Linearization is the idea in calculus where if you zoom in really close onto a section of the graph, the curve and the tangent line will be extremely similar to each other.

We can use this idea and approximate nearby values to the tangent line.

The parent graph of a square root function is
`f(x)=√(x)`.

There are two methods in which we can calculate the approximate value of
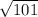`√(101)` by using linearization techniques.

Method 1:

1. Write equation of tangent line.
2. Find the value of y at x = 101.

Let's use the nearest perfect square to
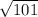`√(101)`, which is
`√(100)`. When drawing the graph of the square root function, we use the point (100, 10) because where x = 100, y = 10 on a square root function.

Now, we have a point that the tangent line passes through, and we want to find the slope.

We can do so by taking the derivative of
`f(x) =√(x)`.

• 
  `f'(x)=x^(1)/(2)`
• 
  `f'(x)=(1)/(2) x^-^(1)/(2)`

• 
  `f'(x)=(1)/(2x^(1)/(2) )`
• 
  `}f'(x)=(1)/(2√(x) )`

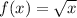Plug in x = 100 to find the slope of the tangent line here.

• 
  `f'(100)=(1)/(2√(100) )`
• 
  `f'(100)=(1)/(2(10))=(1)/(20)`

The slope of the tangent line at x = 100 is 1/20. Now, we can use the point and the slope of the tangent line to determine the equation for the tangent line.

(100, 10), m = 1/20

Point-slope equation:

• 
  `y-y_1=m(x-x_1)`
• 
  `y-(10)=(1)/(20)(x-(100))`
• 
  `y=(1)/(20)x-5+10`
• 
  `y=(1)/(20)x+5`

To find the value of y at x = 101, plug this into the tangent line equation.

• 
  `y=(1)/(20)(101)+5`
• 
  `y=(101)/(20)+5`
• 
  `y=(101)/(20) +(100)/(20) = (201)/(20)`

201/20 is equal to 10.05. Let's estimate the error of this calculation to the actual value of
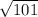`√(101)`, inputted into a calculator.

We get
`√(101)=10.04987562`, which is extremely close to 10.05. Our estimate using linearization only has an error of 0.00012.

Method 2:

You may have noticed that the first method uses little calculus, apart from taking the derivative of f(x).

The more "calculus-y" method involves finding the change in y in terms of the change of x.

We know that dy/dx is the the change in y due to a change in x, so we can use this to find the change in y when x = 101.

• 
  `(dy)/(dx) =(1)/(2√(x) )`

Solve for dy by mutliplying dx to both sides of the equation.

• 
  `dy=(1)/(2√(x) ) \cdot dx`

The change in x is 1, because 101 - 100 = 1.

We want to find the change in y when x = 100, and has a change of 1. Therefore, we have:

• 
  `dx=1`
• 
  `x=100`

Plug these values into the equation
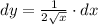`dy=(1)/(2√(x) ) \cdot dx` and solve for dy.

• 
  `dy=(1)/(2√(200) ) \cdot 1`

• 
  `dy=(1)/(2(10))`
• 
  `dy=(1)/(20)`

The change in y when x = 100 with a change of 1 is 1/20. We know when x = 100 the y-value is 10. Therefore, when x = 101, the change in y is 1/20, so y =
`10(1)/(20) = (201)/(20) = 10.05`.

You can see that we get the same answer with either method.