Answer:
Please check the explanation!
Explanation:
Given the polynomial

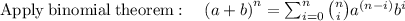
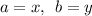
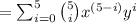
so expanding summation
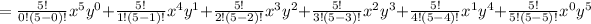
solving
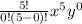
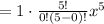
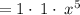
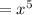
also solving
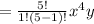


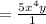
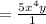

similarly, the result of the remaining terms can be solved such as
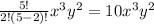
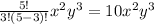
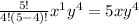
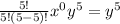
so substituting all the solved results in the expression
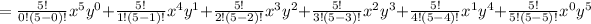
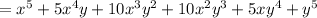
Therefore,
