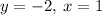Question

A system of linear equations is given by the tables.

Answer 1

Please, see the explanation.

Explanation:

DETERMINING THE EQUATION FOR THE FIRST TABLE

Given the first table

x y

-5 10

-1 2

0 0

11 -22

From the given equation, we can verify and determine that

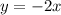`y=-2x` is the required equation that satisfies the table values of the first table.

substituting the table values of all the ordered pairs to check

FOR (-5, 10)

y =-2x

10 = -2(-5)

10 = 10

L.H.S = R.H.S

FOR (-1, 2)

y =-2x

2 = -2(-1)

10 = 2

L.H.S = R.H.S

FOR (0, 0)

y =-2x

0 = -2(0)

0 = 0

L.H.S = R.H.S

FOR (11, -22)

y =-2x

-22 = -2(11)

-22 = -22

L.H.S = R.H.S

As all the ordered pairs of the first table satisfy the equation.

Hence,
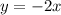`y=-2x` is the equation for the first table.

DETERMINING THE EQUATION FOR THE SECOND TABLE

Given the first table

x y

-8 -11

-2 -5

1 -2

7 4

From the given equation, we can verify and determine that

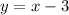`y=x-3` is the required equation that satisfies the table values of the second table.

substituting the table values of all the ordered pairs to check

FOR (-8, -11)

y =x-3

-11 = -8-3

-11 = -11

L.H.S = R.H.S

FOR (-2, -5)

y =x-3

-5= -2-3

-11 = -5

L.H.S = R.H.S

FOR (1, -2)

y = x-3

-2= 1-3

-2 = -2

L.H.S = R.H.S

FOR (7, 4)

y = x-3

4 = 7-3

4 = 4

L.H.S = R.H.S

As all the ordered pairs of the second table satisfy the equation.

Hence,
`y = x-3` is the equation for the second table.

Therefore, the equations are:

`y=-2x`

`y = x-3`

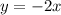
Now, let us solve to determine the solution

`\begin{bmatrix}y=-2x\\ y=x-3\end{bmatrix}`

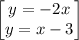
Arrange equation variables for elimination

`\begin{bmatrix}y+2x=0\\ y-x=-3\end{bmatrix}`

`y-x=-3`

`-`

`\underline{y+2x=0}`

`-3x=-3`

`\begin{bmatrix}y+2x=0\\ -3x=-3\end{bmatrix}`

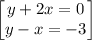
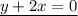
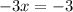
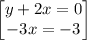
solving

`-3x=-3`

`(-3x)/(-3)=(-3)/(-3)`

`x=1`

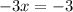
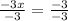
For
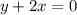`y+2x=0`, plugin
`x = 1`

`y+2\cdot \:1=0`

`y+2=0`

`y=-2`

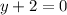
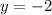
Therefore, the solution to the system of equations are:

`y=-2,\:x=1`