Question

What is an equation of the line that passes through the point

(6,7) and is parallel to the line
2x−3y=9?

Answer 1

The equation of line parallel to given line passing through (6,7) is:
`y = (2)/(3)x+3`

Explanation:

Given equation of line is:

`2x-3y = 9`

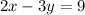
We have to convert the equation in slope-intercept form. The slope-intercept form is given by:

`y= mx+b`

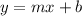
Adding 3y on both sides and subtracting 9 from both sides

`2x-3y+3y-9 = 9+3y-9\\2x-9 = 3y\\3y = 2x-9`

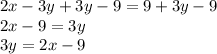
Dividing whole equation by 3

`(3y)/(3) = (2x-9)/(3)\\y = (2)/(3)x - (9)/(3)\\y = (2)/(3)x-3`

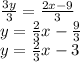
Let m be the slope of given line then

m = 2/3

Let m1 be the slope of line parallel to given line. Slopes of two parallel lines is equal that means:

m = m1 = 2/3

The equation of line will be:

`y = m_1x +b\\y = (2)/(3)x+b`

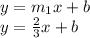
Putting the point (6,7) in equation

`7 = (2)/(3)(6) +b\\7 = 2(2) +b\\7 = 4+b\\b = 7-4\\b = 3`

Putting the value of b

`y = (2)/(3)x+3`

Hence,

The equation of line parallel to given line passing through (6,7) is:
`y = (2)/(3)x+3`