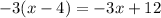Question

Sort each equation according to whether it has one solution, infinitely many solutions, or no solution.

5(x - 2) = 5x - 7
One Solution
Infinitely Many Solutions
No Solution
-30% - 4) =-3x + 12
4(x + 1) = 34+4
-2x - 3) = 2X-6
6(x + 5) = 6x + 11
5) Intro

Answer 1

Equations with one solution:
`-2(x-3) = 2x-6`

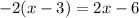
Equations with no solution:

`6(x+5) = 6x+11\\5(x-2) = 5x-7`

Equations with infinite many solutions:
`-3(x-4) = -3x+12`

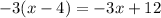
Explanation:

We will solve each equation to see if it has one solution, no solution or infinite many solutions.

An equation where the value of variable can be found has one solution.

An equation with no solution has both sides different.

An equation with infinite solution will have both sides equal after solution(number)

So,

Equation 1:

5(x-2) = 5x-7

`5(x-2) = 5x-7\\5x-10 = 5x-7\\5x-5x = -7+10\\0 = 3`

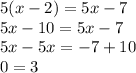
As both sides are not equal, equation has no solution.

Equation 2:

`-3(x-4) = -3x+12\\-3x+12 = -3x+12\\-3x+3x = -12+12\\0=0\\`

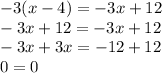
As both sides are equal the equation has infinite many solutions.

Equation 3:

`-2(x-3) = 2x-6\\-2x+6 = 2x-6\\-2x-2x = -6-6\\-4x = -12\\(-4x)/(-4) = (-12)/(-4)\\x = 3`

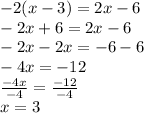
As x=3, the equation has only one solution.

Equation 4:

`6(x+5) = 6x+11\\6x+30 = 6x+11\\6x-6x+30 = 11\\30 =11`

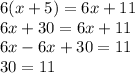
The equation has no solution.

Hence,

Equations with one solution:
`-2(x-3) = 2x-6`

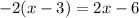
Equations with no solution:

`6(x+5) = 6x+11\\5(x-2) = 5x-7`

Equations with infinite many solutions:
`-3(x-4) = -3x+12`