Answer:
Approximately
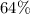 .
.
Step-by-step explanation:
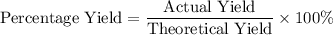
The actual yield of
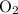 was given. The theoretical yield needs to be calculated from the quantity of the reactant.
was given. The theoretical yield needs to be calculated from the quantity of the reactant.
Balance the equation for the hydrolysis of water:
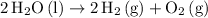 .
.
Note the ratio between the coefficient of
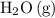 and
and
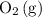 :
:
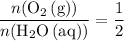 .
.
This ratio will be useful for finding the theoretical yield of
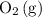 .
.
Look up the relative atomic mass of hydrogen and oxygen on a modern periodic table.
Calculate the formula mass of
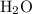 and
and
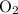 :
:
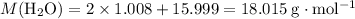 .
.
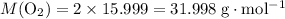 .
.
Calculate the number of moles of molecules in
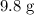 of
of
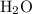 :
:
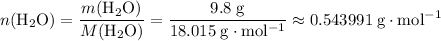 .
.
Make use of the ratio
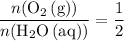 to find the theoretical yield of
to find the theoretical yield of
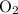 (in terms of number of moles of molecules.)
(in terms of number of moles of molecules.)
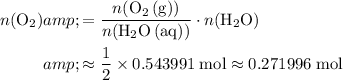 .
.
Calculate the mass of that approximately
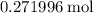 of
of
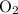 (theoretical yield.)
(theoretical yield.)
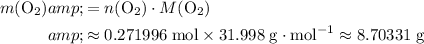 .
.
That would correspond to the theoretical yield of
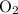 (in term of the mass of the product.)
(in term of the mass of the product.)
Given that the actual yield is
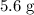 , calculate the percentage yield:
, calculate the percentage yield:
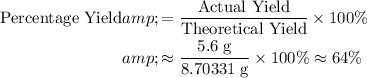 .
.