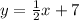Question

Q

ZOO
What is the equation in slope-intercept form of the line that passes through the points
(-6, 4) and (6, 10)?

Answer 1

`y = (1)/(2) x+7`

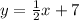
Explanation:

Slope-intercept form: y = mx + b

Slope formula:
`(y2-y1)/(x2-x1)`

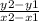
Given points: (-6, 4), (6, 10)

(-6, 4) = (x1, y1)

(6, 10) = (x2, y2)

To write the equation in slope-intercept form, we need to find the slope(m) and the y-intercept(b) of the equation.

First, let's find the slope. To do this, input the given points into the slope formula:

`(10-4)/(6-(-6))`

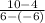
Simplify:

10 - 4 = 6

6 - (-6) = 6 + 6 = 12

`(6)/(12)=(1)/(2)`

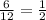
The slope is
`(1)/(2)`.

To find the y-intercept, input the slope and one of the given points(in this example I'll use point (6, 10)) into the equation and solve for b:

`10 = (1)/(2)(6)+b`

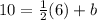
10 = 3 + b

7 = b

The y-intercept is 7.

Now that we know the slope and the y-intercept, we can write the equation:

`y = (1)/(2) x+7`