Answer:
Part (a)
Equation of a circle

where:
- (a, b) is the center
- r is the radius
Given equation:

Comparing the given equation with the general equation of a circle, the given equation is a circle with:
- center = (0, 0)
- radius =
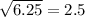
To draw the circle, place the point of a compass on the origin. Make the width of the compass 2.5 units, then draw a circle about the origin.
Part (b)
Given equation:
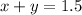
Rearrange the given equation to make y the subject:
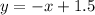
Find two points on the line:
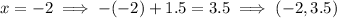
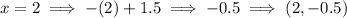
Plot the found points and draw a straight line through them.
The points of intersection of the circle and the straight line are the solutions to the equation.
To solve this algebraically, substitute
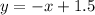 into the equation of the circle to create a quadratic:
into the equation of the circle to create a quadratic:
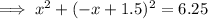
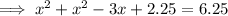
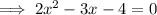
Now use the quadratic formula to solve for x:
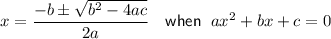
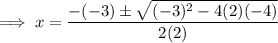
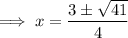
To find the coordinates of the points of intersection, substitute the found values of x into
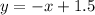
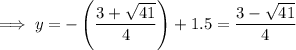
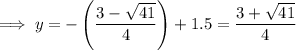
Therefore, the two points of intersection are:
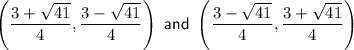
Or as decimals to 2 d.p.:
(2.35, -0.85) and (-0.85, 2.35)