To obtain the least common multiple (l.c.m), we will do it by canonical decomposition or simultaneous decomposition.
This method consists of extracting the common and uncommon prime factors, then
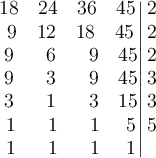
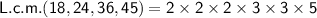
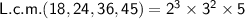

Therefore, the least common multiple of 18, 24, 36 and 45 is 360.