Question

34. The amount of money in an account with continuously compounded interest is given by the formula 1

4 Por, where is the principal, / is the annual interest rate, and / is the time in years, Calculate to the
nearest hundredth of a year how long it takes for an amount of money to double if interest is compounded
continuously at 6,2%Round to the nearest tenth,
11.2 y
A
1 0.0 %
O
4

Answer 1

Explanation:

I have no idea what formula that is you're using but the one I teach in both algebra 2 and in precalculus for continuous compounding is

`A(t)=Pe^(rt)`

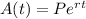
where A(t) is the amount after the compounding, P is the initial investment, ee is Euler's number, r is the interest rate in decimal form, and t is the time in years. If our money doubles, we just have to come up with a number which will be P and then double it to get A(t). It doesn't matter what number we pick to double, the answer will come out the same regardless. I started with 2 and then doubled it to 4 and filled in the rest of the info given with time as my unknown:

`4=2e^((.062)(t))`

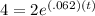
Begin by dividing both sides by 2 to get

`2=e^(.062t)`

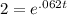
The only way we can get that t out of its current position is to take the natural log of both sides. Natural logs have a base of e, so

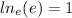`ln_e(e)=1` This is because they are inverses of one another. Taking the natural log of both sides:

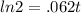`ln2=.062t` Now divide by .062 to get

t = 11.2 years