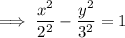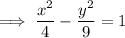Question

1.- What is 'a' for this hyperbola?

2.- What is the slope (as a fraction) for the asymptote with a positive slope. (Use rise/run).


3.- Use the slope of the asymptote to find the 'b' value.


4.- What is the equation for this hyperbola? ​

Answer 1

The standard form of a hyperbola with vertices and foci on the x-axis:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

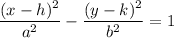
where:

• center: (h, k)
• vertices: (h+a, k) and (h-a,k)
• Foci: (h+c, k) and (h-c, k) where the value of c is c² = a² + b²
• Slopes of asymptotes:
  `\pm\left((b)/(a)\right)`

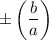
Part 1

The center of the given hyperbola is (0, 0), therefore:

`\implies (x^2)/(a^2)-(y^2)/(b^2)=1`

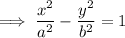
Therefore
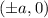`(\pm a,0)` are the vertices. From inspection of the graph,
`a=2`.

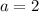Part 2

Choose two points on the asymptote with the positive slope:

(0, 0) and (4, 6)

Use the slope formula to find the slope:

`\sf slope\:(m)=(change\:in\:y)/(change\:in\:x)=(6-0)/(4-0)=(3)/(2)`

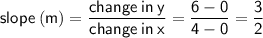
Part 3

Use the slopes of asymptotes formula, compare with the slope found in part 2:

`\implies (b)/(a)=(3)/(2)`

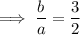
Therefore,
`b=3`

Part 4

Substitute the found values of
`a` and
`b` into the equation from part 1:

`\implies (x^2)/(2^2)-(y^2)/(3^2)=1`

`\implies (x^2)/(4)-(y^2)/(9)=1`