Answer:
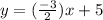
Explanation:
Only one thing you have to remember here and it is the equation for a linear line. This equation is:
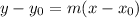
Where m is the slope:
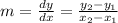
Writing the whole thing out using the given data points we get:
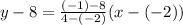
We then just have to equate this to an equation of the form y = mx + b:
⇒
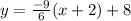
⇒
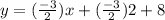
⇒
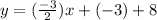
⇒
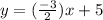
And there we go, our equation has been found.