Question

What is the 8th term of the following sequence?
3/25, 3/5, 3, 5

Answer 1

The 8th term of the following sequence is 9375.

Explanation:

Given the sequence

3/25, 3/5, 3, 15

As we know that a geometric sequence has a constant ratio and is defined by:

`\:a_n=a_0\cdot r^(n-1)`

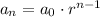
so

`(3)/(25),\:(3)/(5),\:3,\:15`

`((3)/(5))/((3)/(25))=5,\:\quad (3)/((3)/(5))=5,\:\quad (15)/(3)=5`

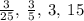
As the ratio 'r' is the same.

so

`r=5`

As the first element of the sequence is

`a_1=(3)/(25)`

Therefore, the nth term is computed by

`\:a_n=a_0\cdot r^(n-1)`

`a_n=(3)/(25)\cdot \:5^(n-1)`

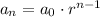
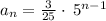
Putting n = 8 to determine the 8th term.

`a_8=5^7\cdot (3)/(25)`

`a_8=(3\cdot \:5^7)/(25)`

`=(5^7\cdot \:3)/(5^2)`

`=5^5\cdot \:3`

`=9375`

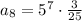
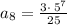
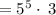
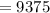
Therefore, the 8th term of the following sequence is 9375.