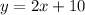Question

write the equation of the line that passes through the points (-3,4) and (-4,2). Write the final answer in slope intecept form

Answer 1

The equation in the slope-intercept form will be:

`y=2x+10`

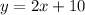
Explanation:

Given the points

• (-3, 4)

• (-4, 2)

Finding the slope between two points

`\left(x_1,\:y_1\right)=\left(-3,\:4\right),\:\left(x_2,\:y_2\right)=\left(-4,\:2\right)`

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`m=(2-4)/(-4-\left(-3\right))`

`m=2`

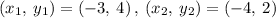
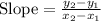
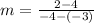
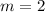
As the point-slope form of the line equation is

`y-y_1=m\left(x-x_1\right)`

putting the values m=2 and the point (-3, 4)

`y-4=2\left(x-\left(-3\right)\right)`

`y-4=2\left(x+3\right)`

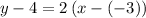
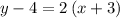
Writing the equation in slope-intercept form

`y=mx+b`

where m is the slope, and b is the y-intercept

so the equation becomes

`y-4=2\left(x+3\right)`

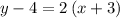
add 4 to both sides

`y-4+4=2\left(x+3\right)+4`

`y=2x+10`

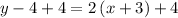
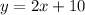
Therefore, the equation in the slope-intercept form will be:

`y=2x+10`