2 Answers

Gajo · Answer 1 · 2023-11-12T16:00:43+0000

Answer:

Let x equal the recurring decimal:

$\sf Equation\:1: \quad x=0.216216216...$

Create another number with recurring 216s by multiplying the above expression by 1000:

$\sf Equation\:2: \quad 1000x=216.216216...$

Subtract Equation 1 from Equation 2 to eliminate the recurring digits after the decimal:

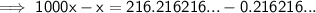
$\sf \implies 1000x-x=216.216216...-0.216216...$

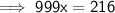
$\sf \implies 999x=216$

Divide both sides by 999:

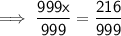
$\sf \implies (999x)/(999)=(216)/(999)$

$\sf \implies x=(216)/(999)$

Simplify:

$\sf \implies x=(216 / 27)/(999 / 27)=(8)/(37)$

Alistair Nelson · Answer 2 · 2023-11-15T10:23:39+0000

Step-by-step explanation:

Let the recurring decimal be x

==========================

x = 0.216216216216...

1000x = 216.216216...

1000x - x = 216

999x = 216

x = 216/999

x = 8/37

Please log in or register to add a comment.