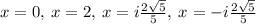Answer:
Please check the explanation.
Explanation:
Given the function
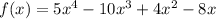
To determine the zeros, set f(x) = 0
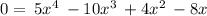
switch sides
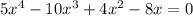
as
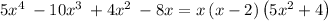
so the equation becomes
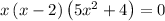
Using the zero factor principle:
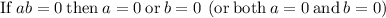
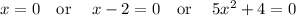
so solving
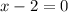
Therefore, the real zeros are:
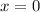 and
and
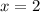
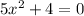 has all the imaginary zeros.
has all the imaginary zeros.
solving
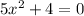
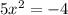
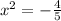
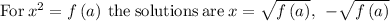
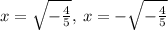
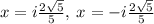 ∵
∵
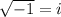
Therefore, the total zeros are: