Question

Consider f(x)=2|x|

What is the rate of change over the interval 0≤x≤4?

How is the rate of change over this interval related to the form of the function?

Answer 1

Please check the explanation.

Explanation:

As we know that the average rate of change of f(x) in the closed

interval [a, b] is

`(f\left(b\right)-f\left(a\right))/(b-a)`

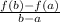
Given the interval [a, b] = [0, 4]

as

`f(x)=2|x|`

`f(b)=f(2)=2\cdot \:4` ∵
`\mathrm{Apply\:absolute\:rule}:\quad \left|a\right|=a,\:a\ge 0`

`= 8`

`f(x)=2|x|`

`f(a)=f(0)=2\cdot \:0` ∵
`\mathrm{Apply\:absolute\:rule}:\quad \left|a\right|=a,\:a\ge 0`

`= 0`

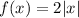
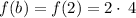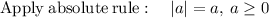
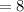
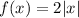
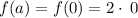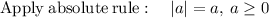
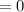
so the average rate of change :

`(f\left(b\right)-f\left(a\right))/(b-a)=(8-0)/(4-0)`

`=(8)/(4)`

`= 2`

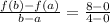
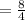
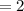
We know that a rate of change basically indicates how an output quantity changes relative to the change in the input quantity. Here, it is clear the value of y increase with the increase of input.