Question

The number of bacteria at the beginning of an experiment was 30 and the bacteria grow at an hourly rate of 1.4 percent. Using the model given by () = 0e, estimate the number of bacteria, rounded to the nearest whole number after 20 hours.

Answer 1

The estimated number of bacteria after 20 hours is 40.

Explanation:

This is a case where a geometrical progression is reported, which is a particular case of exponential growth and is defined by the following formula:

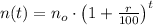`n(t) = n_(o)\cdot \left(1+(r)/(100) \right)^(t)` (1)

Where:

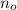`n_(o)` - Initial number of bacteria, dimensionless.

`r` - Increase growth of the experiment, expressed in percentage.

`t` - Time, measured in hours.

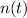`n(t)` - Current number of bacteria, dimensionless.

If we know that
`n_(o) = 30`,
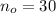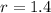`r = 1.4` and
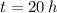`t = 20\,h`, then the number of bacteria after 20 hours is:

`n(t) = 30\cdot \left(1+(1.4)/(100) \right)^(20)`

`n(t) \approx 39.616`

`n(t) = 40`

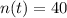
The estimated number of bacteria after 20 hours is 40.