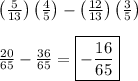Answer: -16/65
Explanation:
Drawing the right triangle (as attached) gives us that
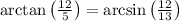
Also,
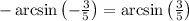
This means our original expression is equal to:
![\cos \left[\arcsin \left((12)/(13) \right)+\arcsin \left((3)/(5) \right) \right]](https://img.qammunity.org/2023/formulas/mathematics/college/29h5fdlfwa2t6wwybhnei92kqrt0mife4g.png)
Using the cosine addition formula, which states
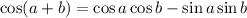 , we get this itself is equal to:
, we get this itself is equal to:
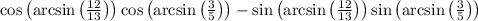
Since
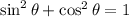 , we know that:
, we know that:
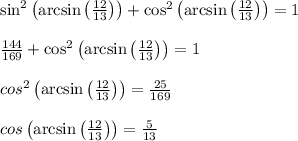
Similarly, cos(arcsin(3/5))=4/5.
This means the given expression is equal to: