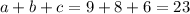Question

Please help!

If we write
`√(2) + (1)/(√(2)) + √(3) + (1)/(√(3))` in the form
`(a √(2) + b √(3))/(c)`, such that
`a`,
`b`, and
`c` are positive integers and
`c` is as small as possible, then what is
`a+b+c`?

Answer 1

`a+b+c=9+8+6=23`

Explanation:

Let’s first simplify our expression. We have:

`\displaystyle {\sqrt2+(1)/(\sqrt2)+\sqrt3+(1)/(√(3))`

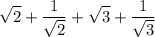
For the second term, multiply both the numerator and denominator by √2. This yields:

`\displaystyle (1)/(√(2))\cdot(√(2))/(√(2))=(√(2))/(2)`

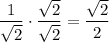
Similarly, for the fourth term, multiply both the numerator and denominator by √3. This yields:

`\displaystyle(1)/(√(3))\cdot(√(3))/(√(3))=(√(3))/(3)`

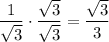
Hence, our expression is now:

`\displaystyle =√(2)+(√(2))/(2)+√(3)+(√(3))/(3)`

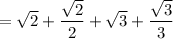
Let’s combine them. First, we will need common denominators.

Our denominators are 2 and 3. So, our common denominator will be its LCM.

The LCM of 2 and 3 is 6.

Hence, let’s make each term’s denominator 6.

For the first term, we can multiply both layers by 6. Hence:

`\displaystyle √(2)=(6√(2))/(6)`

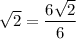
For the second term, we can multiply both layers by 3. Hence:

`\displaystyle (√(2))/(2)=(3√(2))/(6)`

For the third term, we can multiply both layers by 6. Hence:

`\displaystyle √(3)=(6√(3))/(6)`

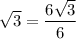
And for the last term, we can multiply both layers by 2. Hence:

`\displaystyle (√(3))/(3)=(2√(3))/(6)`

So, our expression is:

`\displaystyle =(6√(2))/(6)+(3√(2))/(6)+(6√(3))/(6)+(2√(3))/(6)`

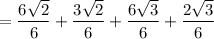
Add:

`\displaystyle =(6√(2)+3√(2)+6√(3)+2√(3))/(6)`

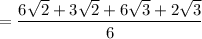
Combine like terms:

`\displaystyle=(9√(2)+8√(3))/(6)`

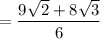
This cannot be simplified. So, c is as small as possible.

Hence: a=9, b=8, and c=6.

Therefore:

`a+b+c=9+8+6=23`