Answer: y =
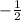 x + 1
x + 1
Explanation:
First, we will find the slope. The slope of perpendicular lines are negative reciprocals.
In this case, the first slope is 2. The negative of 2 is -2, and the reciprocal of -2 is
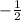 .
.
Now, we will plug in this new slope, the point given, and solve for the b, or the y-intercept.
y = mx + b
(-1) = (
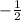 )(4) + b
)(4) + b
-1 = -2 + b
1 = b
Lastly, we will write our equation.
y = mx + b
y =
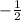 x + 1
x + 1
The line is y =
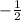 x + 1, or y = 1 -
x + 1, or y = 1 -
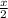 .
.