Question

The slopes of lines PQ and P’Q’ can be determined using the formula m = StartFraction v 2 minus v 1 Over x 2 minus x 1 EndFraction

The product of these slopes is ________. This product shows that the slopes are negative reciprocals. It is given that the lines are perpendicular and we have shown that the slopes of the lines are negative reciprocals.

Answer 1

(a) -- see attached

Explanation:

We're asked to verify that the product of slopes of perpendicular lines is -1. We do that using the given points in the given slope formula.

__

line PQ

The two given points are (a, b) and (c, d). Using these values in the slope formula, we find the slope of PQ to be ...

`m=(y_2-y_1)/(x_2-x_1)=((d-b))/((c-a))`

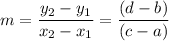
line P'Q'

The two given points are (-b, a) and (-d, c). Using these values in the slope formula, we find the slope of P'Q' to be ...

`m'=(y_2-y_1)/(x_2-x_1)=((c-a))/((-d+b))`

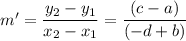
product of slopes

Then the product of the slopes of the two lines is ...

`m* m' = \boxed{\left((d-b)/(c-a)\right)\left((c-a)/(-d+b)\right)=-1}`

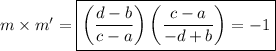
This expression matches choice A.

_____

Additional comment

As is often the case with multiple-choice problems, the only answer choice that is a true algebraic statement is the correct one.