Question

A small object with momentum 7.0 kg∙m/s approaches head-on a large object at rest. The small object bounces straight back with a momentum of magnitude 4.0 kg∙ m/s. What is the magnitude of the large object's momentum change?

Answer 1

The magnitude of the large object's momentum change is 3 kilogram-meters per second.

Step-by-step explanation:

Under the assumption that no external forces are exerted on both the small object and the big object, whose situation is described by the Principle of Momentum Conservation:

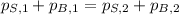`p_(S,1)+p_(B,1) = p_(S,2)+p_(B,2)` (1)

Where:

`p_(S,1)`,
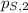`p_(S,2)` - Initial and final momemtums of the small object, measured in kilogram-meters per second.

`p_(B,1)`,
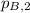`p_(B,2)` - Initial and final momentums of the big object, measured in kilogram-meters per second.

If we know that
`p_(S,1) = 7\,(kg\cdot m)/(s)`,
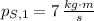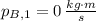`p_(B,1) = 0\,(kg\cdot m)/(s)` and
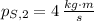`p_(S, 2) = 4\,(kg\cdot m)/(s)`, then the final momentum of the big object is:

`7\,(kg\cdot m)/(s) + 0\,(kg\cdot m)/(s) = 4\,(kg\cdot m)/(s)+p_(B,2)`

`p_(B,2) = 3\,(kg\cdot m)/(s)`

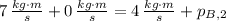
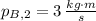
The magnitude of the large object's momentum change is:

`p_(B,2)-p_(B,1) = 3\,(kg\cdot m)/(s)-0\,(kg\cdot m)/(s)`

`p_(B,2)-p_(B,1) = 3\,(kg\cdot m)/(s)`

The magnitude of the large object's momentum change is 3 kilogram-meters per second.