Question

Which inequality represents all values of x for which the quotient below is

defined?
√x+2 / √5-x

A. -2≤x≤5

OB. x2-2

OC. -2
OD. x≤ 5

/ = division

Answer 1

Answer:
`-2 \le x < 5`

========================================================

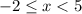
Step-by-step explanation:

We cannot have negative numbers under the square root, if we wanted the result to be some real number.

The stuff under the square root must be 0 or larger.

This means the x+2 must be 0 or larger.

`x+2 \ge 0\\\\x \ge -2`

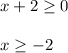
Similarly, the 5-x must be 0 or larger. But wait, we cannot have 0 in the denominator (or else we have a division by zero error), so 5-x must be larger than 0.

5-x > 0

5-x+x > 0+x

5+0 > 0+x

5 > x

x < 5

Combine both
`x \ge -2` and
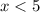`x < 5` to find the domain is
`-2 \le x < 5`

--------------------------------------------------------

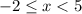
Visual confirmation is shown below. I used Desmos which is a free graphing app.

• f(x) = sqrt(x+2) is in red
• g(x) = sqrt(5-x) is in blue
• h(x) = f(x)/g(x) is in green

The green curve is what we're after. It's between x = -2 and x = 5

We include -2, but exclude 5.

Take note of the closed endpoint at x = -2, and also the vertical asymptote at x = 5. The curve approaches this asymptote but never actually touches it. Think of an electric fence you can get closer to, but not actually touch.