Question

According to the U.S. Census Bureau, 11% of children in the United States lived with at least one grandparent in 2009 (USA TODAY, June 30, 2011). Suppose that in a recent sample of 1640 children, 225 were found to be living with at least one grandparent. At a 2% significance level, can you conclude that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%? Use both the p-value and the critical-value approaches.

Round your answers for the observed value of z and the critival value of z to two decimal places, and the p-value to four decimal places.

Answer 1

The decision rule is

Fail to reject the null hypothesis

The conclusion is

There is no sufficient evidence to show that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%

Explanation:

From the question we are told that

The population proportion is
`p = 0.11`

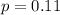
The sample size is n = 1640

The number found to be living with at least one grandparent is
`k = 225`

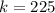
The level of significance is
`\alpha = 0.02`

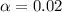
The null hypothesis is
`H_o : p = 0.11`

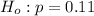
The alternative hypothesis is
`H_a : p > 0.11`

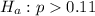
Generally the sample proportion is mathematically represented as

`\^ p = ( k )/(n)`

=>
`\^ p = ( 225 )/(1640 )`

=>
`\^ p = 0.1372`

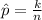
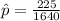
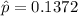
Generally the test statistics is mathematically represented as

`z= \frac{\^ p - p }{ \sqrt{(p(1- p))/(n) } }`

=>
`z = \frac{ 0.1372 - 0.11 }{ \sqrt{(0.11(1- 0.11))/(1640) } }`

=>
`z = 0.0077`

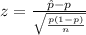
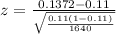
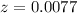
From the z table the area under the normal curve to the left corresponding to 0.0077 is

`p-value = P(Z > 0.0077) = 0.4969`

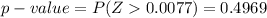
From the value obtained we see that
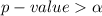`p-value > \alpha` hence

The decision rule is

Reject the null hypothesis

The conclusion is

There is no sufficient evidence to show that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%