Given:
Cost of adult's ticket = $15
Cost of children's ticket = $8
Total tickets = 725
Total sales = $8775
To find:
The number of each type of ticket were sold.
Solution:
Let x be the number of adult tickets and y be the number of children's ticket.
Total tickets :
 ...(i)
...(i)
Total sales :
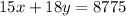 ...(ii)
...(ii)
Multiply equation (i) by 15.
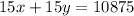 ...(iii)
...(iii)
Subtract (iii) from (ii),



Putting x=-700 in (i), we get
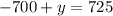
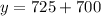
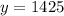
Therefore, the number of adult tickets is -700 and number of child tickets is 1425.
Note: The number of tickets cannot be negative. So, there must be some error in the question.