Answer:
The coordinates of c are (-3,-2)
Explanation:
We have the coordinates of a=(-7,-6) and b=(5,6). We need to find the coordinates of a point c=(x,y) such that:
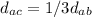
The coordinates x and y have the same relation as the distance:
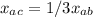
Or, equivalently:
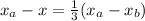
Multiplying by 3:
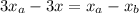
Operating:
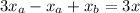
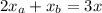
Dividing by 3:
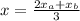
Similarly:
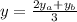
Substituting:
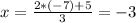
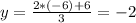
The coordinates of c are (-3,-2)