Question

An endangered species of fish has a population that is decreasing exponentially (A - Apekt). The population 5 years ago was 1800. Today, only 800 of the

fish are alive. Once the population drops below 100, the situation will be irreversible. When will this happen, according to the model? (Round to the nearest
whole year.)
O 12 years from today
15 years from today
O 14 years from today
O 13 years from today

Answer 1

13 years.

Explanation:

I don't understand the original equation you entered, so I'm going to use another one.

`A = A_0e^k^t`

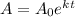
Where A = initial population

A₀ = current population

e = Euler's constant

k = rate of decrease

t = time in years

Let's start off with what we know.

Today there are 800 fish left:

A₀ = 800

There were 1800 fish 5 years ago:

t = -5

A = 1800

The equation now looks like
`1800=800e^-^5^k`

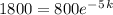
First we find the rate of decrease.

`(1800)/(800) = e^-^5^k`

⇒
`2.25 = e^-^5^k`

⇒
`ln(2.25) = -5k`

⇒
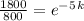
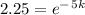
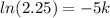
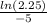`(ln(2.25))/(-5)`=k

⇒ k = -0.1621

The question asks when it will drop below 100, so make it equal to 100.

⇒
`100=800e^-^0^.^1^6^2^1^*^t`

⇒
`100/800=e^-^0^.^1^6^2^1^*^t`

⇒
`ln(1/8)=-0.1621*t`

⇒
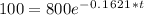
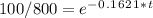
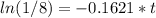
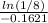`(ln(1/8))/(-0.1621)` = t = 12.821

To the nearest year this is 13.