Question

A red -tailed hawk can travel 50 miles when it flies against the wind In that same amount of time, the hawk can fly 90 miles when flying with the wind. How fast can the red-tailed hawk fly when the wind speed is 10 miles per hour?

Answer 1

Against the direction of the wind is
`x-10=35-10=25\ \text{mph}` and with the wind is
`x+10=35+10=45\ \text{mph}`

Explanation:

Let x be the speed of the hawk in still air

The speed of the wind is 10 mph

So speed of the hawk when flying against the wind is
`x-10` and with the wind is
`x+10`.

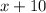Distance the hawk travels when going against the wind is 50 miles and going with the wind is 90 miles

The hawk covers the above mentioned distances in the same amount of time.

`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

`(50)/(x-10)=(90)/(x+10)\\\Rightarrow (50)/(x-10)-(90)/(x+10)=0\\\Rightarrow (50(x+10)-90(x-10))/(x^2-100)=0\\\Rightarrow 50x+500-90x+900=0\\\Rightarrow -40x+1400=0\\\Rightarrow x=(1400)/(40)\\\Rightarrow x=35\ \text{mph}`

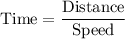
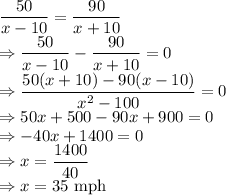
The speed of the hawk in still air is 35 mph.

Speed of the hawk against the direction of the wind is
`x-10=35-10=25\ \text{mph}` and with the wind is
`x+10=35+10=45\ \text{mph}`.